Now according to quantum physics, there is a wave that describes the location of this electron. At any point along the line, the bigger the wave, the more likely the electron is to be found there. Since the electron has to be between A and B, that means the amplitude (size) of the wave outside that interval has to be zero.
This has some very important consequences. One rule of quantum physics is that the wave has to be continuous. That is, it can't have any gaps in it. So this means that in between A and B, the wave has to drop to zero as you get close to A or close to B. This dictates what waves are allowed and what waves aren't allowed between A and B. For example, this wave

is perfectly okay. It's a flat zero outside the region between A and B, and there are no gaps in the wave. But this wave

isn't allowed. There's a big jump at the point B. What makes these two waves different is their "wavelength." This is the distance between the peaks of the wave, and notice that in the second wave, the distance between peaks is shorter than in the first wave. As a result, it doesn't fit right between points A and B.
The wavelength for this electron has to be just right, so that the wave will be zero at the points A and B. This means that only certain waves are allowed. Waves such as these:
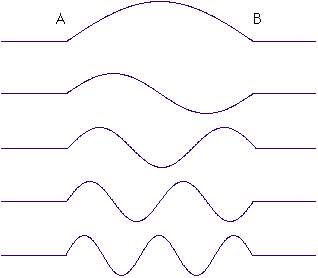
And there are infinitely many more. I've only drawn the five with the longest wavelengths. You can imagine lots of waves with more and more undulations between A and B.
Now the wavelength of a quantum wave is related to the energy that the particle has. I haven't said anything about energy yet, so I should probably define it here. I won't. There are so many different kinds of energy, that to actually sit here and try to define it would be useless. Regarding an electron, though, there are only two kinds of energy that are important. An electron that's has a type of energy associated with its motion, called "kinetic energy." The faster an electron is moving, the more kinetic energy it has. An electron in an atom has a second type of energy, called "potential energy." To see what we mean by potential energy, let's go back and think about gravity again.
Suppose you hold an object high above the ground. If you just hold it there, then it's not moving, so it has no kinetic energy. On the other hand, if you let it go it will start to fall, faster and faster, and by the time it hits the ground it will have quite a bit of kinetic energy. So because you're holding it high above the ground, the object has the "potential" for energy, which is only realized when it falls. That's sort of what we mean by potential energy. The farther from earth (that is, the higher up) an object is, the more potential energy it has.
Of course, you know by now that the electric force works just like gravity (at least mathematically speaking). So an electron inside an atom has potential energy, too. And just as with gravity, the farther an electron is from the nucleus, the more potential energy it has.
So let's get back to our particle in a box. Another rule of quantum physics is that the shorter the wavelength, the higher the particle's energy. And so, since only certain wavelengths can occur for the electron in a box, that means that the energy of the electron can only take on certain values. The electron's energy is said by physicists to be "quantized." That is, it can only occur in certain quantities. This is what gives quantum physics its name.
An electron that's free to roam the universe doesn't have this property. It's energy can take on any value. But any time an electron is confined to a finite region, its energy is quantized. In fact, the smaller the region it's confined to, the farther apart the allowed energy values tend to be. As a result, energy quantization is completely unnoticeable in the solar system, but is very important in an atom.