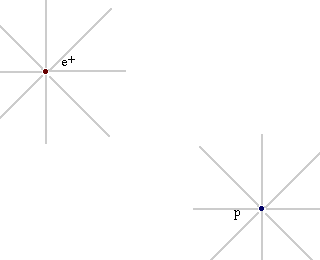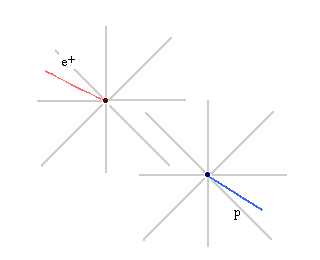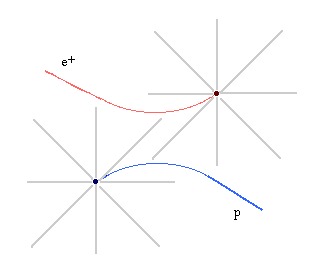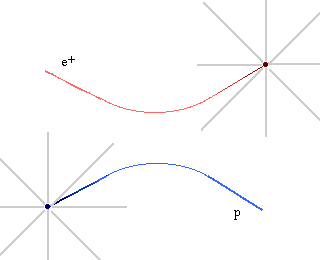
Let's consider an electromagnetic interaction between a proton (p) and a positron (e+). In the "classical" field view of forces, the proton is surrounded by an electromagnetic field. When the positron (or any other electrically charged particle) enters that field, it experiences a force. Similarly, the positron is surrounded by an electromagnetic field, and when the proton enters that field it experiences a force.

But what does quantum physics say about this electromagnetic field?
We need to get sidetracked a bit, onto the subject of light. People have always wondered just what light is. Around 1800, a man named Thomas Young showed that light was a kind of wave. He did this by shining light through very narrow slits, and observing that it spread out afterwards, in a pattern such as only a wave would do. Later in the nineteenth century, James Maxwell, in one of the greatest achievements in all of physics, gathered everything that was known about electricity and magnetism, and a few things that weren't known, into a set of four equations, known today as "Maxwell's equations." (Kind of appropriate, eh?) Anyway, one of the implications of Maxwell's equations turned out to be staggeringly unexpected. Maxwell discovered what kind of wave light is. It's an electromagnetic wave. That is, it's a wave of oscillating electromagnetic fields.
Anyway, for our purpose here, all you really need to know is that electromagnetic fields are made up of particles called photons.
So here's how we now view the interaction between the positron and proton we started to describe above. The positron is surrounded by an electromagnetic field, which really means that it's surrounded by photons which it continually emits and absorbs. As the proton nears the positron, one of these photons is absorbed by the proton. The photon (denoted by the Greek letter gamma in the picture below) has energy and momentum which it carries from the positron to the proton, so that the positron recoils from the loss of energy and momentum, and the proton recoils from the gain. The end result looks about the same, at least for the simple interaction we've described here, but the description of how it happened is different.

Each of the four forces is defined by its gauge boson:
| Electromagnetic force | Photon |
| Strong force | Gluons |
| Weak force | W±, Z0 |
| Gravity | Graviton |
So, for example, any process involving a gluon is a strong force process. Any process involving the weak force will include a W or Z particle (either real or virtual). These gauge bosons are said to "mediate" the corresponding forces.
Here are a couple more examples of processes involving subatomic particles, displayed in their full quantum mechanical glory, with virtual particles.
Muon decay. (The decay products are an electron, a muon neutrino, and an electron anti-neutrino. By tradition, photons and the W's and Z are represented by wavy lines. Far be it from me to break with tradition.)
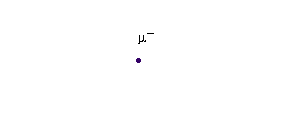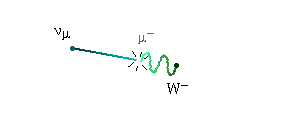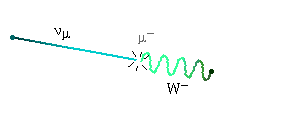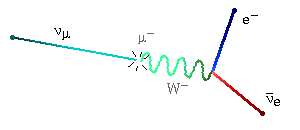
Electron-positron annihilation. (In this one, the two photons produced are real. The virtual particle is the "middle electron.")
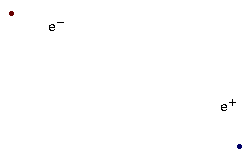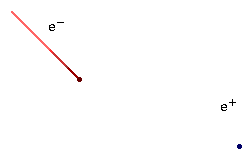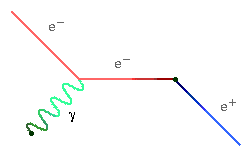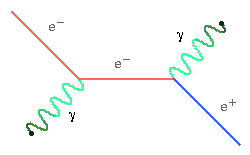
The first of these is a weak force process, while the second is an electromagnetic process. You can tell this because the first one contains a W particle, while the second one contains photons.
So this is how things happen in the microcosmos. And now that we know that, we can look at each of the four forces in a little more detail.