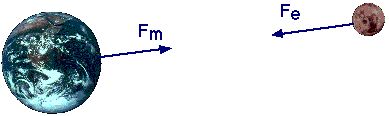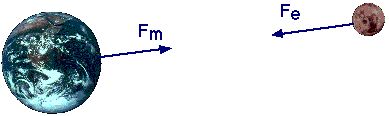The Classical Picture of Forces
All these particles we've introduced interact with each other by way of the four forces I've mentioned. To understand how these particles interact with each other, it's probably best if we look at different ways in which the concept of "force" can be viewed.
Action at a Distance
The simplest way in which we can describe an interaction between two objects is simply to say that one of them exerts a force on the other. For example, let's consider the interaction between the earth and the moon.
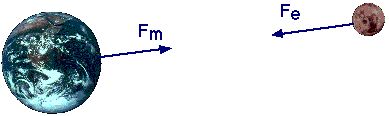
The earth exerts a gravitational force on the moon (Fe) while the moon exerts a gravitational force on the earth (Fm). By Newton's third law of motion, these forces are of equal strength and in opposite directions. However, many people (including Newton) have been reluctant to accept this idea of "action at a distance." Such people are bothered by the idea that the earth could directly exert a force on an object over 200,000 miles away. (The distance is irrelevant, really, but the point is, the earth isn't touching the moon.) An alternate way that doesn't rely so much on action at a distance is to think of a force in terms of "fields."
Fields
Instead of thinking of the earth and the moon directly exerting forces on each other, we can introduce a middle man, called a "gravitational field." Here's how it works. We think of the earth as being surrounded by a gravitational field which extends outwards in all directions for a great distance. (Technically, forever, but it gets weaker the farther we go out.) Then this gravitational field exerts a force on anything that's in it, such as the you or me, or the moon.
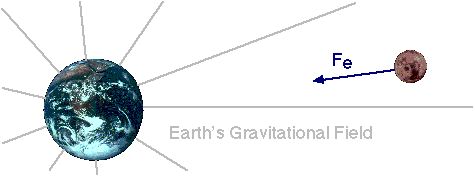
The moon (and any other object with mass) is also surrounded by a gravitational field, and any object, such as the earth, in that field experiences a force as well. (I've left this out of the picture above, though. Too much clutter, otherwise.)
We can look at electric forces the same way. Consider, for example, the electric force between a proton and an electron. We can say that the proton is surrounded by an electric field, and this electric field exerts a force on the electron. and the electron is surrounded by an electric field, which exerts a force on the proton.
Either way, the result is the same. The moon experiences the same force, regardless of what we consider to be the immediate source of that force, the earth, or a gravitational field. So do these fields really exist? Well, they're not tangible, certainly, but they do seem to have some important features. For example, a fluctuating electric field creates a magnetic field, and a fluctuating magnetic field creates an electric field. So these fields sort of have a life of their own. This is especially true when we consider the consequences of quantum physics.
The Quantum Picture of Forces
Previous page
Dave's Microcosmos