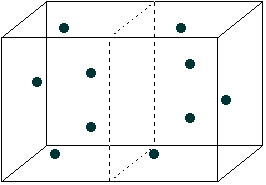

I've divided the box in half with a dashed line. The molecules in this box
will be zipping around very fast, bouncing off the walls, off each other, and
so forth. As a result, they'll be distributed randomly throughout the box. Right
now, the number of molecules in the left half of the box is about the same as
in the right half. But it doesn't have to be that way.
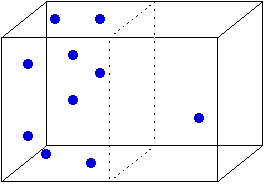
Here, 9 of the 10 molecules are on the left side of
the box. What are the odds of that happening? About one in 102. (Where did
that number come from?) On the other hand, the odds of half the molecules
being on each side is about one in 4. We can express this in terms of microstates
and macrostates. The macrostate with 9 molecules in the left half has 10 microstates
(each of which has a different molecule on the right). The macrostate with 5
molecules on each side has 252 microstates. In other words, the macrostate with
5 molecules on each side has a higher entropy than the one with 9 molecules
on the left. And since all microstates are equally likely (each molecule has
the same chance of being on the left or the right) a macrostate with higher
entropy (more microstates) is more likely than one with lower entropy. In the
case of the two macrostates shown above, the one with the even distribution
is about 25 times as likely (252/10) as the one with the uneven distribution.
As we consider boxes with more particles, the preference for an even
distribution gets much much stronger as the number of microstates in a macrostate
explodes. For example, suppose we have a box with 1000 molecules. The number
of microstates with 500 molecules on each side is about 10^299 (that is, 1 followed
by 299 zeroes) while the number of microstates with 900 molecules on one side
of the box is only about 10^140. So the former macrostate has a much larger
entropy than the latter, and is about 10^159 times as likely. And if that seems
like an astronomical number, keep in mind that when it comes to the number of
molecules in a gas, 1000 doesn't even begin to describe it. The number of air
molecules in a shoebox is around 10^22. So when we have a house full of air,
we can expect the molecules to distribute themselves pretty evenly throughout.
Such a state has a much greater entropy, and so is much more likely to occur.
So go ahead wander into the kitchen to get yourself a cold one. There'll be
plenty of air when you get there. Probably.
Entropy and energy
The Page of EntRoPy
![]() Back to Dave's Physics Shack?
Back to Dave's Physics Shack?
Here's where that number (and some of the others) came
from. Each molecule can be in either the left or the right half. That's two
possibilities, and with 10 particles the total number of possibilities is 2^10
= 1024. Now of those 1024 possibilities, 10 of them have 9 molecules on the
left. (The one on the right can be any one of the 10 molecules.) So the odds
of having 9 molecules on the left is 10/1024, or about 1 in 102.
The same idea lies behind the other numbers, but it takes factorials
to actually calculate them. For example, to calculate the number of microstates
with 90 molecules on one side and 10 on the other, we calculate 1000!/(900!
100!) =6.4 x 10^139. If you've ever played with factorials before, you know
they get very big very fast. So when I say that one macrostate is more likely
than another, I mean really really more likely!
Back to where you where you were?