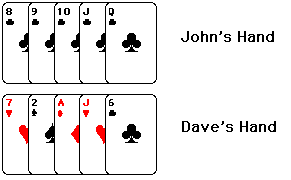

For those of you not familiar with poker, John's hand is one of a type called
a "straight flush." (A straight flush consists of five cards in a
row, of the same suit.) As you might guess, it's considered a very good hand.
Dave's got the type of hand which is sometimes called "junk" by the
more refined poker players. (I usually have stronger language for it.)
John will most likely savor this moment, for it is a rare one indeed.
A player receiving Dave's cards will most likely be unimpressed, knowing that
this hand is as common as dirt. But is it?
The chances of being dealt John's hand out of a thoroughly shuffled deck
of cards is about one in 2.6 million. On the other hand, the chances of being
dealt Dave's hand is........ about one in 2.6 million!
The chances of receiving any particular five cards in a deal from
a shuffled deck of cards is the same. There are about 2.6 million five card
hands that you can make out of a standard 52 card deck, and each of them is
equally likely.
So why is John surprised to see his hand, while Dave isn't surprised
to see his?
Because John's hand is one of a very select group of hands, called a
straight flush. Out of the 2.6 million possible hands, there are only 40 straight
flushes. Dave has junk. There are over a million hands that are junk. In other
words, there are very few combinations of five cards that form a straight flush.
There are very many combinations of five cards that result in junk.
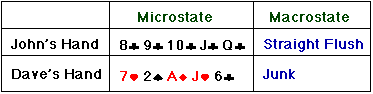
Now here's a little terminology we can use to describe the state of a
poker hand. The particular combination of five cards that make up a hand we
call the "microstate" of that hand. If we group all the possible hands
into classes, such as "full house" and "three of a kind"
, we call these classes "macrostates."
For example,
Entropy (Remember entropy? This is a web page about entropy.) is defined
in terms of these macrostates and microstates. Specifically, the entropy of
a macrostate is equal to the natural logarithm of the number of microstates
in that macrostate, times a number called Boltzmann's constant. (Ludwig Boltzmann
was the first person to define entropy in this manner.) So the more microstates
in a macrostate, the greater the entropy. A straight flush has only forty microstates,
so it has a low entropy, while junk has over a million microstates, so it has
a high entropy.
Now here's the key point that leads to the second law of thermodynamics.
Every single possible microstate of our system is equally likely. This is true
whether we're talking about John and Dave's poker hands, or a glass of water,
or the interior of a neutron star. As a result, the most likely macrostate of
a system is the one with the most microstates. There are over 25,000 times as
many junk hands as straight flushes, so a junk hand is over 25,000 times as
likely. In other words, the most likely macrostate of a system is the one with
the greatest entropy.
So the reason John is surprised to see his cards while Dave is not surprised
is that John's hand is in a very rare macrostate, while Dave's hand is in a
very common macrostate. We expect to see high entropy hands like Dave's junk
(with many microstates) and not low entropy hands like John's straight flush.
High entropy hands are more common than low entropy hands, simply because there
are more of them. If we buy a new deck of cards, we can immediately deal two
straight flushes right off the top of the deck. (The cards in a new deck are
all in order.) The entropy of the cards is low. When we shuffle the deck, the
entropy increases. We start dealing lousy, high entropy, hands. As you learn
more about entropy, you'll see that increasing entropy is the way of the world.
In the meantime, next time you play poker, take the time to savor those lousy
hands. Each one is just as rare as a great one.
Entropy and a box of air
The Page of EntRoPy
![]() Back to Dave's Physics Shack?
Back to Dave's Physics Shack?