The Copenhagen Interpretation

"Those who are not shocked when they first come across quantum theory cannot possibly have understood it." ---Niels Bohr
Anyone who has studied quantum physics will agree that it's very strange. Not only do we not know everything we would like to know about a particle, but we can't know everything we would like to know. This is what the uncertainty principle tells us. But there are many areas of science that are strange, and this is not the most unique feature of quantum physics. What makes quantum physics truly special is this: Even if we know the theory of quantum physics inside out, and we perform thousands of experiments that verify its predictions, there are still questions that remain. These questions involve the meaning, the interpretation of quantum physics. For example, if we can't know the position or momentum of a particle, does the particle even have a specific value of position or momentum? Or does the particle only have these attributes when we measure them? The surprising answers provided by quantum physics seem to be: no and yes. To illustrate this, let's go back again to Young's two slit experiment.

The Two Slit Experiment Rerevisited

Remember, it goes like this. Young shone light through two very narrow slits, very close together, onto a screen. The light wave emerging from one slit interfered with the wave emerging from the other slit, and the result was not two narrow stripes of light (one for each slit) but a whole series of stripes that we call an interference pattern. Now let's consider this in terms of photons, particles of light. You might expect it to work as follows. We shine the photons at the slits, some go through one slit, some through the other. The photons emerging from one slit interfere with the photons emerging from the other, and we get an interference pattern. Now suppose we make the light very dim, and replace the screen we use to observe the result with a photographic film, thus giving us a permanent record of the light striking the screen. Dimmer light means fewer photons, and if the light's dim enough we can actually see the impact of the individual photons on the film. Instead of stripes, we get very tiny spots where the photons hit, but the spots arrange themselves into the interference pattern. That is, the places where we would have bright stripes if the light were brighter, are the places we see most of the photons hitting. Where the dark stripes would be, we get very few photons. One can conceivably make the light so dim that photons pass through the slits one at a time. Physicists have actually done this! And as the spots accumulate on the film, the interference pattern appears.

And there's the problem. If we send just one photon at the slits, and it passes through one slit or the other, what is there for it to interfere with when it emerges? There must be interference because if we do this over and over again, an interference pattern emerges. However, if the photon passes through one slit, there's nothing coming out of the other slit!

The only way to resolve this is to go back to wave thinking again. The wave­particle passes through both slits, and the result that emerges from each slit interferes with the result from the other slit. It's more than simply saying we don't know which slit the photon passes through. The photon doesn't pass through just one slit at all. In other words, as the photon passes through the slits, not only don't we know it's location, it doesn't even have a location. It doesn't have a location until we observe it on the film. This paradox is the heart of what has come to be called the Copenhagen interpretation of quantum physics.

The Copenhagen Interpretation

Now I should start out here with a disclaimer. Nobody has ever really, as far as I know, set down an "official" version of the Copenhagen interpretation of quantum physics. (If you know differently, me a line!) If you ask ten different physicists what the Copenhagen interpretation is, you'll get nine similar (but not exactly the same) answers, and one "Who cares?" The interpretation of quantum physics is a bit out of the mainstream of physics education, because students are too busy learning how to calculate stuff. So what I'm going to call the Copenhagen interpretation is really just my interpretation of the Copenhagen interpretation. The situation's a bit unfortunate, but there it is.

The Copenhagen interpretation concerns how much we can know about a particle, and when. One of the central features of quantum physics, relative to this, is called the "collapse of the wave function." (When I say "wave function", just think "wave." Physicsist use the phrase "wave function" because it sounds more technical. :-) In the two slit experiment, after the wave-particle passes through the slits, we have a wave that is spread out over a broad region, meaning that the photon could be discovered anywhere. When it hits the film and makes a spot, this is no longer the case. We now have the location of the photon narrowed down to a very small region, which means that its wave function must be restricted to that region also. A sudden change like this in a wave, due to a measurement (in this case, the film "measures" the location of the photon), is the collapse of the wave function. The exact mechanism behind this collapse is not really known, and in my opinion the collapse of a wave function is the central mystery of quantum physics.

I'll summarize the Copenhagen interpretation of quantum physics this way:

  1. The wave function is a complete description of a wave-particle. That is, any information that can't be derived from the wave function doesn't exist. For example, if the wave is spread out over a broad region, then we can't determine where the particle is located. And since the wave function doesn't tell us the location, the particle doesn't have a location. Similarly, if a wave is made up of many different momenta, then the wave-particle doesn't have a value for the momentum.
  2. When a measurement of a wave-particle is made, its wave function collapses. So for example, if we precisely measure the momentum of a particle, its wave function suddenly changes from a wave made up of many momenta, to a wave with only one momentum. (This is termed a collapse, even though the wave doesn't actually get any smaller in this case. Remember, a wave with an exact momentum extends across the entire universe.)
  3. If two properties of a wave-particle are related by an uncertainty relation (such as the Heisenberg uncertainty principle), no measurement can simultaneously determine both properties to a precision greater than the uncertainty relation allows. In the case of the Heisenberg uncertainty principle, this means that if we measure the position of a particle, then there's a limit to the precision with which we can know the momentum. A consequence of this is that when we measure the position of a particle, we affect its momentum, and vice versa.
We can illustrate this last tenet of the Copenhagen interpretation, again with light passing through a narrow slit. The wave property of light dictates that when light passes through a slit, it doesn't travel straight through, but spreads out as it emerges from the slit.

Light rays spread out after passing through a slit.

If we imagine a single photon passing through the slit, the slit "measures" the position of the photon. (That is, as the photon passes through the slit, its location must be somewhere within the region denoted delta-x in the picture. This measurement of the position of the photon introduces an uncertainty in the momentum of the photon, reflected in the fact that the photon is no longer moving straight ahead, but is moving at an unknown angle. The uncertainty in momentum is labeled delta-p in the diagram, and delta-x deltap must be large enough to satisfy the Heisenberg uncertainty principle.

The Bohr-Einstein Debate

The Copenhagen interpretation derives its name from its leading exponent, the Danish (hence "Copenhagen") physicist Niels Bohr. Bohr, among his many contributions to quantum physics, was the central figure in clarifying the implications of quantum physics in the early part of the twentieth century. He did this largely in response to a series of challenges by quantum skeptic (despite his role in the creation of the theory) Albert Einstein. These challenges, and Bohr's responses, are collectively referred to as the "Bohr-Einstein Debate."

This was not a debate with two lecterns and a moderator. It was just an informal give and take over the course of several meetings between Bohr and Einstein. A typical encounter would consist of Einstein devising a hypothetical experiment for precisely measuring both the position and momentum of a particle at a particular moment, in violation of the uncertainty principle. Bohr would then examine the experiment in more detail, and discover that there was no inconsistency to the uncertainty principle after all.

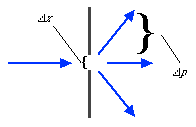
An example may prove instructive. I don't think this is actually an argument brought up by Einstein, but it's close to one of his, and it's in the same spirit. It involves a photon and a slit (you're probably getting sick of this by now, but photons and slits are so useful in explaining quantum physics). The slit has a width delta-x, and so it measures the position of the photon to that accuracy. The difference here is that the slit is allowed to slide freely back and forth. The measurement of the position of the photon by the slit alters the momentum of the photon in the direction parallel to the width of the slit by an amount consistent with the uncertainty principle:

.

But there's another law of physics called the Law of Conservation of Momentum. In our case, this law implies that if the momentum of the photon changes due to passing through the slit, the momentum of the slit changes by an exactly opposite amount (i.e. it recoils).

So if we measure the recoil momentum of the movable slit, we get a measurement of the momentum of the photon. And in principle, we can make the slit smaller and smaller, until eventually the uncertainty principle is violated.

The problem here is that we've applied the uncertainty principle only to the photon, and not to the slit. We are measuring the momentum of the photon parallel to the width of the slit by measuring the momentum change of the slit. This can only work if we know what the momentum of the slit is to start with, and we know it at least as precisely as we're trying to measure. Hence, the uncertainty in the momentum of the slit as the photon passes through must satisfy

And the slit must satisfy the Heisenberg uncertainty principle, which means there's an uncertainty in the position of the slit which satisfies

And finally, since the only thing we know about the location of the photon is that it passes through the slit, any uncertainty in the location of the slit is an uncertainty in the location of the photon:

We can then deduce from these three equations that

And we see that this measurement is fully consistent with the Heisenberg uncertainty principle! This is how the Bohr-Einstein debate went. Each time Einstein proposed an experiment to beat the uncertainty principle, Bohr managed to show that there was no inconsistency after all. In the end, Einstein was forced to concede that quantum physics was at least consistent. (That's right, Einstein lost the Bohr-Einstein debate!)

And so, as strange as its consequences may seem, quantum physics, including the Heisenberg uncertainty principle, stands up under the most thorough theoretical scrutiny (such as the Bohr-Einstein debate) and experimental scrutiny (a whole other story, perhaps for another time) that physicists have been able to muster. In the end, we are left with uncertainty.

Previous page
The Page of Uncertainty