From Many Waves, One
(I'm hoping you can stop these waves somehow with your browser once you've taken in the motion. If you can't, I'm sorry for the distraction.*)
The mathematical prototype of a wave,

is shown here only in part. It really extends infinitely far to the left and right. But in quantum physics this wave is supposed to describe an electron (or some other waveparticle). Now a subatomic particle is a small thing and typically isn't spread out over the entire universe. So the perfect wave above, while possessing the virtue of mathematical simplicity, doesn't really describe what we think of as a particle. A more appropriate wave might look something like this:
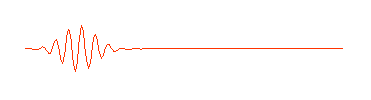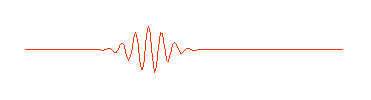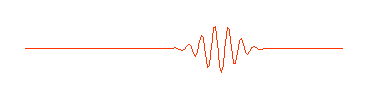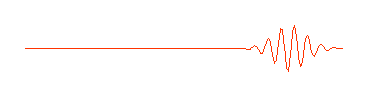
Physicists call this a "wave packet." Now remember, that the amplitude (size) of the wave in any region determines the probability of finding the particle there. If we can perform an experiment which would actually reveal where the particle is, we would be more likely to find it near the center of the wave packet, where the amplitude of the wave is largest, rather than out near the ends of the packet, and we certainly wouldn't expect to find it out beyond the ends of the wave packet. The particle is somewhere in the wave packet, but we don't know exactly where.
Next, let's consider the momentum of this waveparticle. De Broglie, Davisson, and Germer showed that the momentum of the particle is related to the wavelength of the wave (the distance between successive peaks in our wave, remember). For the wave at the top of the page, that extends across the entire universe, this is not a problem. But for the wave packet below it, the question of wavelength is not so simple. The distance from one wave to the next is not exactly the same everywhere, and beyond the wave packet, where the wave dies out, the whole idea of wavelength becomes a bit hazy.
It turns out, however, that this problem was worked out mathematically by Jean Baptiste Joseph Fourier, early in the nineteenth century. To illustrate Fourier's discovery, here's a rather strange looking wave:
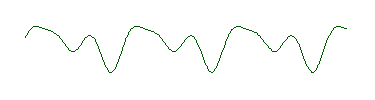
It doesn't have the shape of the "perfect" wave at the top of the page. However, this wave is in fact the sum of these three waves:
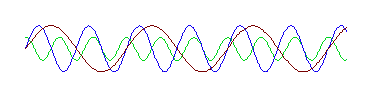
That is, if we take these three waves and add them up, we get the strange wave. And notice that each of these three waves has the same shape as the "perfect" wave prototype at the top of the page. In other words, the strange wave does not have a single wavelength, but is made up of waves with three different wavelengths. (If you have some graphing software, even a spreadsheet, you can verify this for yourself. The three perfect waves are described mathematically by sin(x), sin(2x) and .5cos(3x), and you can verify that the strange wave is the sum of these three functions.)
What Fourier showed was that any wave, no matter how bizarre can be described as a sum of perfect waves with different amplitudes and wavelengths. It may take an infinite number of these perfect waves, but it can be done.
So the wave packet shown near the top of this page, which could represent the wave of an electron for example, doesn't have a single wavelength. It's a wave with a combination of lots of different wavelengths. And this fact is what leads to the Heisenberg uncertainty principle.
The Heisenberg Uncertainty Principle
Previous page
The Page of Uncertainty
*You see, I had just downloaded "GifBuilder," this great piece of freeware for making animated gifs, and, well, I was making this web page about waves, and I just figured, why not make waves that move, instead of the usual static ones you find in all the textbooks, because, after all, this is the web, and if everything on your web page just sits there, you're not really with it, are you?
Back




