The rewrite of this page was inspired by an email exchange with David Melcher.
I get a fair amount of email from people with questions about time dilation and length contraction. Much of it is from astute readers who ask some variation on the following question:
In Astro's frame of reference, it's Nevals's clock that's moving, and so it's Nevals's clock that should run slow. Therefore, from this point of view, if the trip takes 39 hours in Nevals's frame, it should take longer in Astro's frame. What's wrong with that logic?It's always good news and bad news when I get a question like this. It's good news in that the reader is thinking, and in fact it shows that the reader is "getting it." The bad news for me is that the answer is complicated. Anyway, here's where I'll attempt to answer it.
We'll do another example. Again, more spaceships and planets. (Examples in relativity require very high speeds, which means you have to use very large distances if you don't want microscopic times. Hence, planets and spaceships.) These two planets, A and B, are located 12 light years apart. There's a clock on A and a clock on B that are synchronized so that they read the same time.
A spaceship flies by planet A on a line towards planet B, passing A at the exact moment when the clock on A reads zero. (Either a wild coincidence, or perhaps they knew the ship was coming.) The spaceship moves at .8 light speed.
Let's start with what happens in the planets' reference frame. In that frame, the ship moves at .8 light speed. The two planets are 12 light years apart, and so the time it takes to get there is equal to the distance divided by the speed, which gives us 15 years. In other words, as the ship flies by planet B, the clocks on A and B read 15 years. (I'm having the ship fly by the planets, rather than taking off and landing, to simplify things.) So far, so good.
Now we'll look at things in the ship's frame, this time in more detail than before. In the ship's frame, the distance from A to B is shrunk by a factor of gamma:
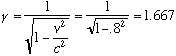
So the distance is 12 light years divided by 1.667 = 7.2 light years. Then the time it takes is the distance divided by the speed, .8 c, which gives us 9 years, instead of the 15 it takes in the planets' frame. There's your time dilation.
Now let's stay in the ship's frame and look at what happens with the clocks A and B. And here's the crucial point. The people on planet A and B have synchronized their clocks. But that synchronization only holds in the planets' reference frame. In the ship's frame these two clocks don't read the same. When we say two clocks are synchronized, we mean that Clock A and Clock B read zero at the same time. But one crucial feature of relativity is that two events at two different locations that are simultaneous in one reference frame are not simultaneous in a different reference frame. In the ship's frame of reference, Clock A and Clock B read zero at different times. (Usually when relativity seems to be contradicting itself, the concept of simultaneity is involved somehow.)
If you do the math (*), you find that in the ship's reference frame, as the ship passes planet A, Clock A reads zero at the same time that Clock B reads 9.6 years. Years later, as the ship passes planet B, Clock B reads 15 years at the same time that Clock A reads 5.4 years (more math **).
And now here's where we bring it all together. (This is gonna be neat.) In the ship's frame of reference, Clocks A and B are both moving. Therefore, we expect these clocks to be running slow, due to time dilation, by a factor of gamma. So while the 9 years go by on the ship's clock, we expect that the time elapsed on the planets' clocks should be 9/gamma = 5.4 years. Which is exactly what we have in the previous paragraph!
So you see, people in each reference frame observe that the clocks in the other frame are going slow. And yet it all somehow manages to be consistent, because of the fact that events that appear simultaneous in one reference frame are not simultaneous in another. Whew!
Anyway, if you were confused about time dilation after Astro's adventure, I hope this has cleared things up a bit. And if you weren't confused, I hope you still aren't!
* The math involves what's called a Lorentz transformation, which relates positions and times in one reference frame to positions and times in another. It looks like this:
In this equation, v is the relative speed of the two reference frames (.8 c here), x and t are the position and time of an event in the planets' reference frame, and x' and t' are the position and time of an event in the ship's reference frame. So we ask ourselves, when t' (the ship's time) is zero, what is the time t at the location of Planet B? You take the second equation, put in 0 for t', put in 12 light years for x (the location of Planet B), and solve for t. You get 9.6 years. In other words, as the ship passes Planet A, Clock A reads 0 at the same time that Clock B reads 9.6 years. Even though in the planets' reference frame these clocks are synchronized!
** Again, we figure this using the Lorentz transformation above. This time we want to know what time Clock A is reading at the same time (in the ship's frame) that Clock B reads 15 years. So we take the second equation in the Lorentz transformation, and plug in 0 for x (the location of Planet A), 9 years for t' (remember, that's how long the trip takes in the ship's frame), and find t. You find that t is 5.4 years. In other words, as the ship passes Planet B, Clock B reads 15 years at the same time that Clock A reads 5.4 years.