Space and Time

We've arrived at a paradox. The rule that we've described for translating velocities in one reference frame to another frame, "common sense relativity", is not consistent with Einstein's second postulate that the speed of light is the same in all inertial reference frames. There are only two ways for this to be true. Either distances are different from one inertial frame to the next, time is different from one frame to the next.

In fact, both of these things are true. The first effect we call "length contraction" while we call the second effect "time dilation".

Length Contraction

Length contraction is sometimes referred to as Lorentz contraction, or Lorentz-FitzGerald contraction. The mathematical formula for describing it was arrived at by Lorentz and Fitzgerald before Einstein, but it took Einstein to fully understand its significance and embed it into a complete theory of relativity. The principle is this:
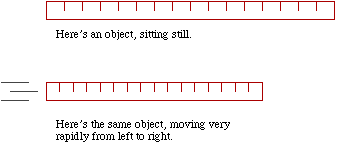
The length of an object in a frame in which it is moving is shorter than the length of the same object in a frame in which it's at rest.
An illustration may make this less confusing:

In the top illustration, we view the ruler in the reference frame in which it is at rest. The length of an object in its own rest frame is called its "proper length". The proper length of a yardstick is one yard. In the lower illustration, the ruler is moving. In longer, more complicated words, we view the ruler from a reference frame in which the ruler is moving. The principle of length contraction says that the ruler is shorter in this frame.

This contraction is not an illusion. Any accurate experiment we might devise to measure the length of this ruler as it moves past us will reveal a shorter length than the object has at rest. The ruler doesn't just look shorter when it's moving. It is shorter! However, it's only shorter along the direction it's moving. In the second illustration above, the ruler is moving horizontally, and it's shortened horizontally. You might notice that vertically, it's the same size in both illustrations.

Time Dilation

The effect called time dilation is similar to length contraction, and it works like this:
The time between two events, in a frame in which those events occur at different locations, is longer than the time between those same two events, in a frame in which those events occur at the same location.
This one's a bit more confusing. Again, I'll try to illustrate.

Either of these clocks can be used to measure the time it takes the first clock to travel from point A to point B. However, the two clocks will give different results. We can think of it this way. The two events we're talking about are the clock leaving point A, and the clock arriving at point B. In our frame, these events take place at different points (A and B). However, let's look at this from the reference frame of the upper clock. From this point of view, the upper clock is at rest (anything is at rest from its own point of view) and the bar containing the points A and B is rushing by from right to left. So the two events, the departure of point A and the arrival of point B both take place at the same point: the point where the clock sits! (The time measured by the upper clock is called the "proper time".) By the principle stated above, the lower clock will register a longer time than the upper clock as the upper clock moves from point A to point B.

A simpler, less precise way of stating this principle is:

A moving clock runs more slowly than a stationary clock.
The most famous hypothetical illustration of time dilation is usually called the twin paradox. Suppose there are twins named Harry and Mary. Mary takes off in a spaceship which travels very fast away from earth (it must travel close to the speed of light for the effect to be noticeable) and returns very fast. We can think of the human body as a clock which records the passage of time by aging. Since Mary is moving very fast, her clock runs slowly, compared to Harry's clock. As a result, when Mary arrives back at earth she has aged less than Harry has. How much less depends on how far she has traveled, and how fast.

Time dilation is not just a crazy idea. It has been verified experimentally. Perhaps the best example of this involves a subatomic particle called a muon. The muon is an unstable particle, which means that shortly after one is created, it decays into lighter particles. How long a muon takes to decay has been measured very precisely. Anyway, it's been observed that a muon moving close to the speed of light lives longer than a muon that's at rest or moving slowly. This is a relativistic effect. From the point of view of the moving muon it doesn't live any longer, because from its point of view, it's at rest. It's only in the frame of the laboratory through which the muon moves that the lifetime is lengthened, or "dilated".

I should add at this point that there are many, many other tests of the ideas we've seen so far, and of the other implications of relativity that we'll see later. My point is, even though it's still often referred to as the "theory" of relativity, don't think that this implies that special relativity is in doubt. It's very well established.

The gamma factor
Dave's relativity page
Previous page