Relativity Before Einstein

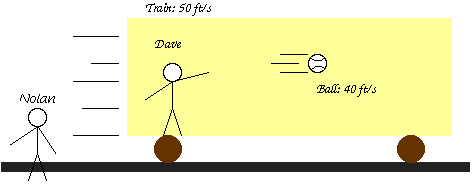
Here we have a railroad car. Train

Let's suppose for the moment that the railroad car is not moving. Dave (on the train) throws a baseball to the right at 40 feet per second (ft/s). This means that after one second, the ball is 40 feet in front of him. (We'll ignore gravity, and assume the car is at least 41 feet long..)

Now we put the train in motion. The train is moving in a straight, level line at a steady 50 ft/s. Dave goes through the exact same motion that would produce a 40 ft/s throw in the stationary train. The moving train is an inertial frame of reference, so Einstein's first postulate says that life on the moving train is just like life on the train at rest. Specifically, if Dave goes through exactly the same motion, the ball will be 40 feet in front of him after one second, whether the train is moving or not.

Next, we'll consider the flight of the ball from Nolan's point of view. Suppose that at the instant Dave throws the ball, Dave and Nolan are side by side. Since the train is moving at 50 ft/s, after one second Dave is 50 feet ahead of Nolan. And of course, the ball is 40 feet in front of Dave. So after one second, the ball is 90 feet (40 + 50) ahead of Nolan.

In other words, from Nolan's point of view the ball is traveling 90 ft/s.

To summarize,

(Are you starting to see why this is called "relativity"?)

Mathematically, we write it this way:

.
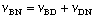The three relative velocities in this equation are just those listed immediately above. (You can match them up from the subscripts for "ball", "Dave", and "Nolan".) The basic idea is that to get the velocity of the ball in a second reference frame (Nolan's), we take the velocity of the ball in the first reference frame (Dave's) and we add or subtract (depending on the directions of things) the relative velocities of the two frames. This insight is often attributed to Galileo, and is sometimes referred to as "Galilean relativity". I sometimes refer to it as "common sense relativity", since we were able to sit down and reason it out just using common sense. (This is not to belittle the achievements of Galileo Galilei, who was one of the finest scientific minds ever seen.) In fact, the logic by which we arrived at this equation is so simple and so reasonable, that it's hard to imagine that it could be wrong.
Einstein's seond postulate
Dave's relativity page
Previous page
P.S. Speaking of Nolan, if you're a baseball fan, you may have heard a cliche to the effect that "a pitcher pitches with his legs as much as his arm" or some such statement. The idea behind this is relativity, as I've described it above. As the pitcher releases the ball, its velocity relative to the ground is equal to the velocity of the hand relative to the body (generated by arm strength) plus the velocity of the body relative to the ground, which is generated by the back leg (the right leg for a right-handed pitcher). In other words, if you can get your body moving an extra 5 mph towards the plate by pushing off the pitching rubber with your back foot, that's an extra 5 mph on your fastball!

Nolan Ryan, for example, (I'm not positive this is true, so don't quote me on this) used to drive his body forward so hard and so far with his back foot that by the end of a game his right knee would sometimes be dirty from scraping it on the pitcher's mound. This is an important part of the reason why Ryan's fastball was once clocked at 100.8 mph, and why he could throw 95 mph well into his 40's.