

This is the English translation of a webpage originally written in French, by Nymbus, who also provided the translation. I've agreed to post it here at my own website, and have cleaned up the translation a bit, editing for grammar, and so on, but leaving the content untouched, I think. So any comments or questions should be addressed to . It's his project. (Although, if there's a problem with the page such as the images not showing up or special characters not appearing, send word to .) --DaveThis page has also been translated into Spanish.
At times, this page alludes to concepts from the special theory of relativity, which are explored here.
Before beginning this brief article, dealing with the essential features of general relativity, we have to postulate one thing: special relativity is supposed to be true. Hence, general relativity lies on special relativity. If the latter were proved to be false, the whole edifice would collapse.
In order to understand general relativity, we have to define how mass is defined in classical mechanics.
The two different manifestations of mass:
First, let's consider what represents mass in everyday life: "It's weight." In fact, we think of mass as something we can weigh, as that's how we measure it: we put the object whose mass is to be measured on a balance. What's the property of mass we use by doing this? The fact that the object and Earth attract each other. To be convinced of it, just go in your garage and try to raise your car! This kind of mass is called "gravitational mass." We call it "gravitational" because it determines the motion of every planet or of every star in the universe: Earth's and Sun's gravitational mass compels Earth to have a nearly circular motion around the latter.
Now, try to push your car on a plane surface. You cannot deny that your car resists very strongly to the acceleration you try to give it. It is because the car has a very large mass. It is easier to move a light object than a heavy one. Mass can also be defined in another way: "It resists acceleration." This kind of mass is called "inertial mass."
We thus arrive at this conclusion: we can measure mass in two different ways. Either we weigh it (very easy...) or we measure its resistance to acceleration (using Newton's law).
Many experiments have been done to measure the inertial and gravitational mass of the same object. All lead to the same conclusion: the inertial mass equals the gravitational mass.
Newton himself realized that the equality of the two masses was something his theory couldn't explain. But he considered this result as a simple coincidence. On the contrary, Einstein found that there lay in this equality a way to supplant Newton's theory.
Everyday experimentation verifies this equality: two objects (one heavy and the other one light) "fall" at the same speed. Yet, the heavy object is more attracted by Earth than the light one. So, why doesn't it fall "faster"? Because its resistance to acceleration is stronger. From this, we conclude that the acceleration of an object in a gravitational field doesn't depend upon its mass. Galileo Galilei was the first one to notice this fact. It is important that you should understand that the fact that all objects "fall at the same speed" in a gravitational field is a direct consequence of the equality of inertial and gravitational masses (in classical mechanics).
Now, I would like to focus on the expression "to fall." The object "falls" because of Earth's gravitational field generated by Earth's gravitational mass. The motion of the two objects would be the same in every gravitational field, be it Moon's or Sun's. They accelerate at the same rate. It means that their speeds increase by the same value in every second. (Acceleration is the value by which speeds increases in one second).
The equality of gravitational and inertial masses as an argument for Einstein's third postulate:
Einstein was looking for something which could explain this: "Gravitational mass equals inertial mass."
Aiming at this, he stated his third postulate, known as the principle of equivalence. It says that if a frame is uniformly accelerated relative to a galilean one, then we can consider it to be at rest by introducing the presence of uniform gravitational field relative to it.
Let's consider a frame K', which has a uniformly accelerated motion relative to K, a galilean frame. There are many objects around K and K'. These objects are at rest, relative to K. So, these objects, relative to K', have a uniformly accelerated motion. This acceleration is the same for all objects, and it is opposed to the acceleration of K' relative to K. We have just said that all objects accelerate at the same rate in a gravitational field. So, the effect is the same as if K' is at rest and that a uniform gravitational field is present.
Thus, if we state the principle of equivalence, the equality of the two masses is a simple consequence of it. That's why this equality is a powerful argument in favor of the principle of equivalence.
By supposing K' is at rest and a gravitational field is present, we make of K' a galilean frame, where we can study the laws of mechanics. That's why Einstein stated his fourth principle:
Einstein's fourth postulate:
Einstein's fourth postulate is a generalisation of the first one. It can be expressed in the following way: "The laws of nature are the same in every frame." It cannot be denied that it is more "natural" to say that the laws of nature are the same in every frame than in galilean ones. Moreover, we don't really know if a galilean frame really exists.
The deadly lift:
Let's consider a lift in free fall, falling within a very high skyscraper. A foolish man is inside it.
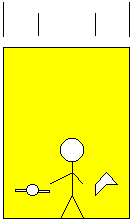
The man lets his watch and his handkerchief fall. What happens? For someone watching the fall from outside the lift, whose frame is Earth's, the watch, the handkerchief, the man and the lift fall at exactly the same speed. (Let's remember that the motion of a body in a gravitational field doesn't depend upon its mass, according to the equivalence principle.) Thus, the distance between the watch and the floor, or between the handkerchief and the floor, or between the man and the watch, or between the man and the floor... doesn't vary. Therefore, for the man inside the lift, the watch and the handkerchief will stay where he left them.
Now, if the man gives his watch or his handkerchief a certain speed, they will follow a straight line at a constant speed. This leads to the following conclusion: the man inside the lift can ignore Earth's gravitational field. The lift behaves like a galilean frame. However, it will not last forever. Sooner or later, the lift will crash, and the observer outside the lift will attend to a great slaughter!
Now, let's do a second idealized experiment: our lift is far away from any great mass, in deep space for example. Our foolish man has survived his accident, and, after several years in a hospital (years, with respect to what?...), he decides to go back in the lift. Suddenly, a being (what kind of being, we don't know, ask Mulder for the answer) begins to pull the lift:
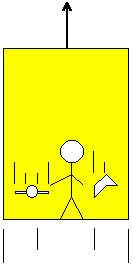
Classical mechanics tells us something: a constant force provokes a constant acceleration. (This is not true at very high speeds, as the mass of an object increases with its velocity; however, we will consider it as true for our experiment.) Hence, the lift will have an accelerated motion in any galilean frame.
Our guinea pig inside the lift lets his handkerchief and his watch fall. Someone outside the lift in a galilean frame thinks that the watch and the handkerchief will hit the floor, as the latter will catch up with them because of its acceleration. In fact, the observer outside the lift will see the distance between the watch and the floor and the distance between the handkerchief and the floor diminish at the same rate. On the other hand, the man inside the lift will notice that his watch and his handkerchief have the same acceleration. He will attribute it to a gravitational field.
These two interpretations seem equally true: on the one side, an accelerated motion, on the other side, a uniform motion and the presence of a gravitational field.
Let's do another test to justify the presence of a gravitational field. A ray of light gets into the lift through a window and hits the wall facing it. Here are the two interpretations of our observers:
The one outside the lift tells us: "Light gets into the lift though the window horizontally in a straight line and at a constant speed (of course!) toward the opposite wall. But the lift is going upward: thus, the light will hit the wall not exactly in front of its entry point, but a little bit lower."
The man inside the lift says: "I am in presence of a gravitational field. As light has no mass, it will be spared the field's effects, and it will hit the wall exactly in front of its point."
Oops! A problem! The two observers don't agree. However, the man inside the lift has made a mistake. He said that light has no mass. But lights carries energy, which has a mass (remember the mass of a Joule of Energy is: M=E/c2...). Hence, light will have a curved trajectory towards the floor, as the observer outside the lift said.
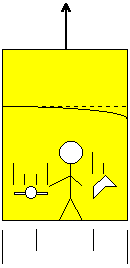
As the mass of energy is very small (c2 = 300 000 000 * 300 000 000!), the phenomenon can only be detected in the presence of VERY strong gravitational fields. It has been verified thanks to the sun's great mass: rays of light are curved when they approch it. This experiment was the first confirmation of Einstein's theory.
All these experiments allow us to conclude: we can consider that an accelerated frame is a galilean one by introducing the presence of a gravitational field. Furthermore, it is true for all kinds of motions, be they rotations (the gravitational field explains the presence of centrifugal forces) or not uniformly accelerated motions (which is translated mathematically by the fact that the field doesn't satisfy Riemann's condition). As you see, the principle of general relativity is fully in accordance with experience!
NB: This example is drawn from "L'évolution des idées en Physique" (Champs Flammarion 1982) written by Albert EINSTEIN and Leopold INFELD. A marvelous book! Read it if you have any interest in physics in general. Fascinating!
Universe's geometry:
Now, things are going to be very very weird. I'm sure you were astonished when you discovered time dilation. But Einstein also discovered another strange consequence of his postulates: the world in wich we live is not Euclidean (in most cases). This means that circles are not round, that parallel lines can cross or diverge and that the angles of a triangle may not add up to 180°!
But be careful! I don't say that what you learned at school is false! Euclidean geometry, as a mathematical abstraction, is always true. But when it comes to describing the real world, nothing is sure. Before Einstein discovered that Euclidean geometry was not the one which described the world, Gauss and later Riemann developed another kind of geometry. It is sometimes called "Gaussian geometry." When they developed this new branch of math, they couldn't even imagine that it was to be the proper description of the world. In fact, Einstein, helped by his friend Grossman (a good mathematician) developed his general theory of relativity on the basis of Gaussian geometry. What I want to show is that math is developed without any reference to the world. It's an "abstraction."
Let's take another example: 1+1=2. Is it true? As a mathematical abstraction, always true. But when you want to give this expression a physical meaning, it is sometimes false. For instance, you cannot add the speed of light to another speed (remember the experience with the train, we couldn't add the speed of photons to the speed of the train): "v + c = c." If you add one liter of milk to one liter of water, you will not obtain 2 liters of liquid. Do you see what i mean? Math is certain as long as they don't refer to reality. It is very important that you should understand this. Now, let's go back to general relativity.
Let's consider a huge disk above which are drawn two concentric circles, one very small and the other one as huge as the disk:
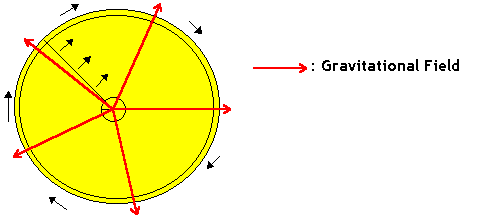
Our observer is on the disk, which rotates at a very high speed. Another man, in a galilean frame, measures the circumferences (P) of the two circles, and their diameters (d) with a ruler. This man then does the following calculus: P/d. He finds: P/d = p. For him, euclidean geometry is true. (True means here that it describes reality.)
The observer on the disk measures the circumferences and the diameters WITH THE SAME RULER. For the measurement of the diameters, the ruler is not contracted (from the point of view of the man in the galilean frame) in its length. (See special relativity for this.) Thus, the observer on the disks will find the same results as the man in the galilean frame.
Now, the observer measures the circumference of the small circle. For the man outside the disk, the rule is not contracted in its length because it goes very slowly (it's close to the center of the disk). Therefore, the observer finds again the same result.
However, things are going to be different for the fourth measurement. When the observer on the disk measures the circumference of the big circle, he goes very fast compared to the man outside the disk. Hence, from the point of view of this man, the rule is contracted in its length and the observer won't find the same result. For him: P/d does not equal p. Euclidean geometry doesn't describe reality in this case.
What can account for this strange result? The observer on the disk, when measuring the circumference of the big circle, experienced a strange force. You would call it a "centrifugal force." It's due to the presence of a gravitational field (symbolized on the diagram by arrows).
The same experiment could be done to measure time by using a clock in the three different frames: in the galilean frame, on the disk close to its center and far from it. It would lead us to the same conclusion: When the observer on the disk is far from its center, his measurement of time is different from the man's outside the disk. The presence of a gravitational field could account for the difference.
This leads us to the following conclusion: a gravitational field influences time and space.
Time dilation due the presence of a gravitational field has been measured. In fact, the value of this field at the top of a high moutain is slightly less than its value at the bottom of the moutain. Two atomic clocks initially synchronised gave two different results after having spent a while in these two different places:
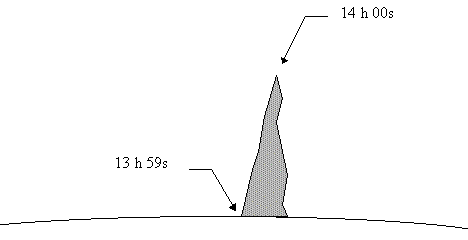
Conclusion:
I hope you have appreciated this brief introduction to general relativity. If you have any comments, please .