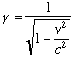
The answer is that the effect depends on how fast you're going, and you're going very slow. (You and that Missouri State Trooper may think you're driving fast, but as far as the theory of relativity is concerned, you're driving very slow.) The effects of time dilation and length contraction are only noticeable if you're traveling close to the speed of light, which is about 186,300 miles per second (or 300,000,000 meters/second).
Mathematically, relativistic effects are described by a factor which physicists normally denote by the Greek letter gamma. This factor depends on the speed at which an object is traveling. For example, if a meter stick (proper length 1 meter) is moving past us very rapidly, its length in our reference frame is 1 meter divided by gamma. If a clock traveling from point A to point B measures 3 seconds during its trip, then in our reference frame, the trip takes 3 seconds times gamma.
To see why we never notice relativistic effects in real life, let's look at the formula for gamma:
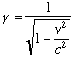
The key here is the v2/c2 in the denominator. v is the velocity of the object we're talking about, while c is the speed of light. Since the velocity of any normal-sized object is much less than the speed of light, v/c is very small, and when we square this it's smaller still. So, gamma is, for all practical purposes, 1 for any normal sized object you've ever seen. And since we calculate relativistic effects by multiplying or dividing by gamma, at normal speeds lengths and times are virtually unchanged. To illustrate this, here's a table of the value of gamma for different speeds. The last column is the length of a meter stick moving at this speed, in meters. (This is just 1 meter, divided by gamma.)
| Speed | Speed (miles/hour) | Gamma | Length |
| 0 | 0 | 1 | 1 |
| 20 meters/second | 45 | 1.0000000000000022 | .9999999999999978 |
| 100,000 m/s | 224,000 | 1.000000056 | .999999944 |
| .1 c (30 million m/s) | 67 million | 1.005 | .995 |
| .9 c | 600 million | 2.29 | .44 |
| .999 c | 670 million | 22.4 | .045 |
| c | 670 million | Infinite | 0 |